Steel02

Steel02#

Steel02 is a uniaxial material based on the Giuffre-Menegotto-Pinto formulation with added isotropic strain hardening by [FilippouEtAl1983].

Model.uniaxialMaterial("Steel02", tag, Fy, E, b, R0, cR1, cR2[, a1, a2, a3, a4, sigInit])

Add a Steel02 material to model identified by tag.

Parameters:

  • tag (int) – integer tag identifying material

  • Fy (float) – yield stress, \(F_y\) [1]

  • E (float) – initial elastic tangent, \(E\) [1]

  • b (float) – strain-hardening ratio, \(b\)

  • R0 (float) – parameter to control the transition from elastic to plastic branches, \(R_0\)

  • cR1 (float) – parameter to control the transition from elastic to plastic branches, \(cR1\)

  • cR2 (float) – parameter to control the transition from elastic to plastic branches, \(cR2\)

  • a1 (float) – isotropic hardening parameter (optional: default = 0.0).

  • a2 (float) – isotropic hardening parameter (optional: default = 1.0).

  • a3 (float) – isotropic hardening parameter (optional: default = 0.0).

  • a4 (float) – isotropic hardening parameter (optional: default = 1.0).

  • sigInit (float) – Initial Stress Value (optional: default = 0.0)

class Steel02#
Fy: float#

Yield stress \(F_y\).

E: float#

Initial stiffness \(E\). Analogous to E in the Elastic material.

Formulation#

The hardening formulation was developed by [FilippouEtAl1983]. The parameters a1 and a2 increase of compression yield envelope as proportion of yield strength after a plastic strain of \(a_2 F_y/E\).

The parameters a3 and a4 increase of tension yield envelope as proportion of yield strength after a plastic strain of \(a_4 F_y/E\).

Typical values are R0 between 10 and 20, cR1=0.925, cR2=0.15

../../../../../_images/Steel02-Backbone.png

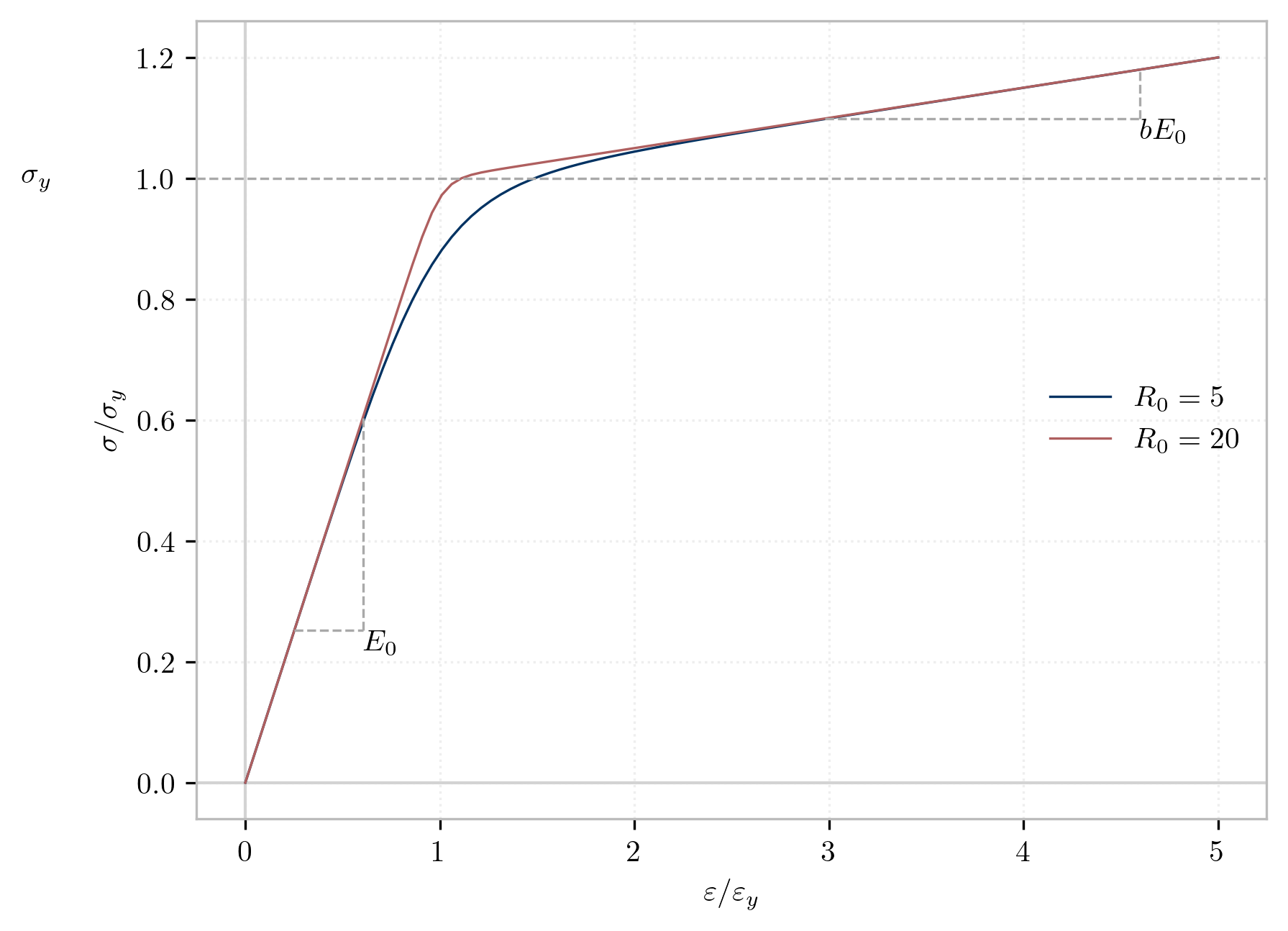
Steel02 monotonic envelope#

../../../../../_images/Steel02-Cycling.png

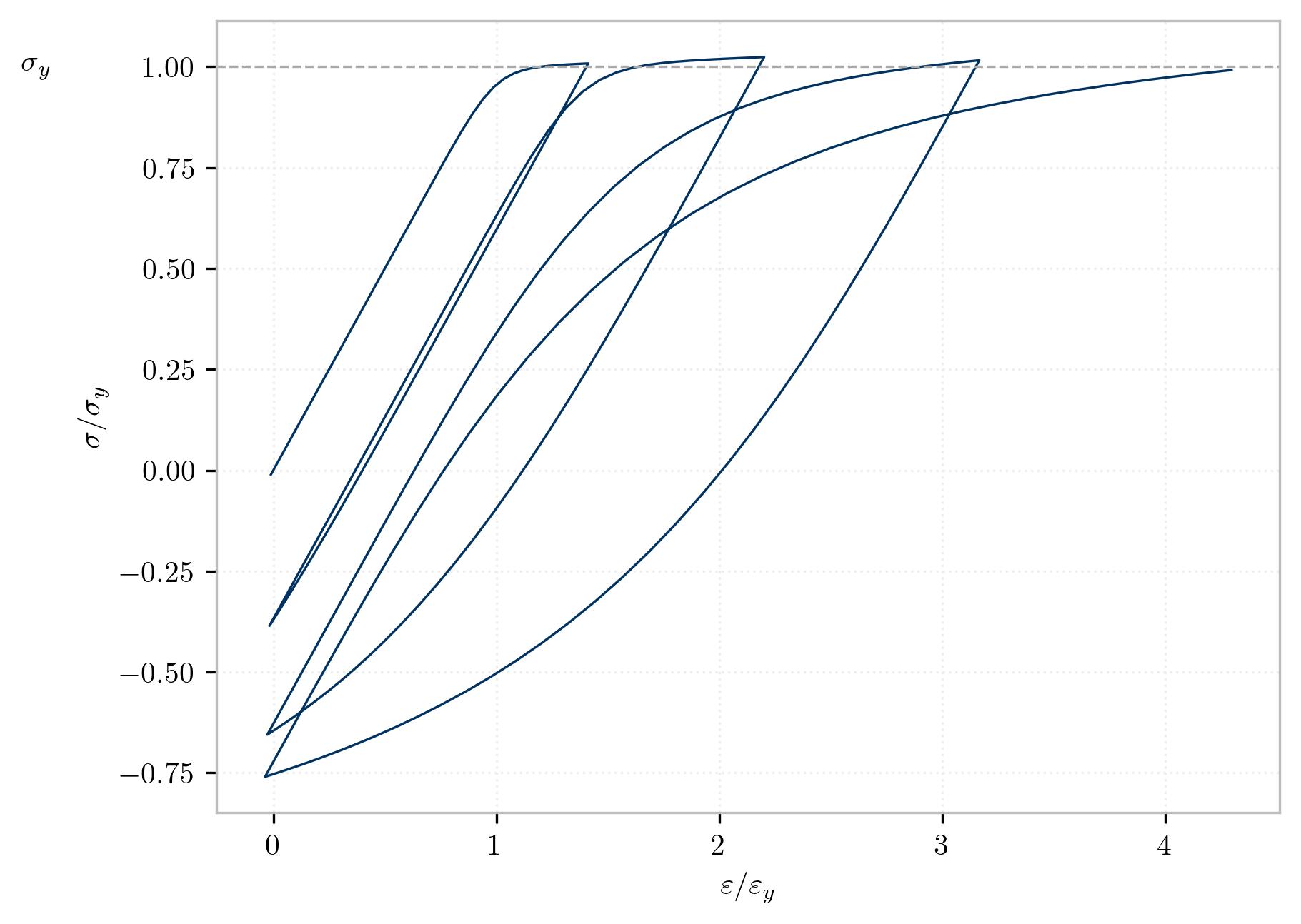
Hysteretic behavior without isotropic hardening#

cite{goldberg1963analysis} proposed a curve which furnishes the stress explicitly in terms of strain, as expressed below:

\[\bar{\sigma}(\bar{\varepsilon}) = b{\bar{\varepsilon}} + \frac{(1-b){\bar{\varepsilon}}}{\left(1 + |{\bar{\varepsilon}}|^r\right)^\frac{1}{r}},\]

where \(\bar{\sigma}=\sigma/F_y\), \(\bar{\varepsilon}=\varepsilon/\varepsilon_y\), \((F_y, \varepsilon_y)\) is the yield point, \(b\) is the strain hardening parameter, and the parameter \(r\) influences the shape of the transition curve and takes account of the Bauschinger effect. A hysteretic loading-reloading algorithm for this curve was proposed by cite{giuffre1970comportamento}, which was extended by cite{filippou1983effects} to include isotropic hardening.

Example#

The following example defines a Steel02 material with tag 1, a yield stress of 60.0 and an initial tangent stiffness of 30000.

model.uniaxialMaterial('Steel02',1, 60.0, 30000.0, 0.1, 20.0, .925, .15)

References#

[FilippouEtAl1983] (1,2)

Filippou, F. C., Popov, E. P., Bertero, V. V. (1983). “Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints”. Report EERC 83-19, Earthquake Engineering Research Center, University of California, Berkeley.

Code Developed by: Michael H. Scott, fcf

Contents